Lượng giác chiếm khá nhiều lượng kiến thức trong môn toán ở bậc THPT, đây cũng là một trong những phần kiến thức quan trọng để ôn thi THPT quốc gia vì vậy mà bài viết này nhằm hệ thống lại các công thức lượng giác một cách đầy đủ để các bạn ôn lại kiến thức nhằm phục vụ cho việc giải các bài toán ứng dụng trong tam giác nói riêng và hình học nói chung
Vài nét về lịch sử Lượng giác:
Lượng giác (tiếng Anh: Trigonometry) là một nhánh toán học dùng để tìm hiểu về hình tam giác và sự liên hệ giữa cạnh của hình tam giác và góc độ của nó.
Nguồn gốc của lượng giác được tìm thấy trong các nền văn minh của người Ai Cập, Babylon và nền văn minh lưu vực sông Ấn cổ đại từ trên 3000 năm trước. Các nhà toán học Ấn Độ cổ đại là những người tiên phong trong việc sử dụng tính toán các ẩn số đại số để sử dụng trong các tính toán thiên văn bằng lượng giác. Lagadha là nhà toán học duy nhất mà ngày nay người ta biết đã sử dụng hình học và lượng giác trong tính toán thiên văn học trong cuốn sách của ông Vedanga Jyotisha, phần lớn các công trình của ông đã bị tiêu hủy khi Ấn Độ bị người nước ngoài xâm lược.
Nhà toán học Hy Lạp Hipparchus vào khoảng năm 150 TCN đã biên soạn bảng lượng giác để giải các tam giác.
Một nhà toán học Hy Lạp khác, Ptolemy vào khoảng năm 100 đã phát triển các tính toán lượng giác xa hơn nữa.
Nhà toán học người Silesia là Bartholemaeus Pitiscus đã xuất bản công trình có ảnh hưởng tới lượng giác năm 1595 cũng như giới thiệu thuật ngữ này sang tiếng Anh và tiếng Pháp.
Bảng công thức lượng giác đầy đủ:
1) Giá trị lượng giác của 1 góc:
2) Cung liên kết (Cos đối, Sin bù, phụ chéo)
.JPG)
3) Công thức lượng giác cơ bản
4) Công thức cộng
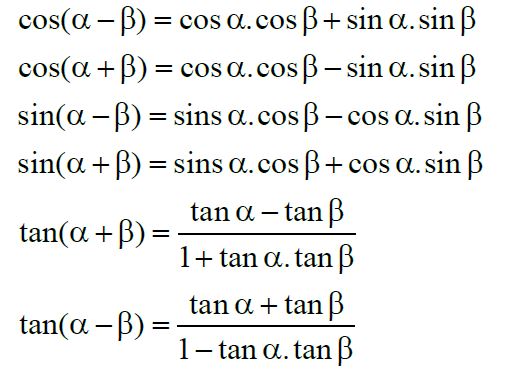5) Công thức nhân đôi, nhân ba
6) Công thức hạ bậc
7) Công thức biến đổi tổng thành tích
8) Công thức biến đổi tích thành tổng
Chúc các bạn học tập thật tốt!
_jpg/263x165_crop_thanh-pho-cho-cong-nghe-2-(1).jpg "Những thành phố hàng đầu cho phái đẹp mê công nghệ tại Mỹ")
_jpg/263x165_crop_cong-nghe-tra-luong-cao-1-(1).jpg "Những hãng công nghệ trả lương cao tại Mỹ")
